This is a short presentation of the main results.

In Dictionary Learning, signal representation is obtained with the aid of dictionary atoms, a set of vectors which form an overcomplete basis. The concept of infinite atoms, proposed in AsyDiL, extends the notion of an atom to that of an infinite set, with the aim of achieving more accurate signal representations; since a set of atoms covers more space than an individual vector, more signal properties can be captured in this way.

We have proposed two methods for implementing the infinite atoms: a probabilistic approach, which considers the variance around a mean atom following a Gaussian distribution and a geometric approach, which defines the infinite set as a hypersector (or cone) determined by a central atom and a radius. The figure below provides a visual illustration of the two approaches, showing how a given signal can be represented with two atoms (left: Gaussian, right: cones).

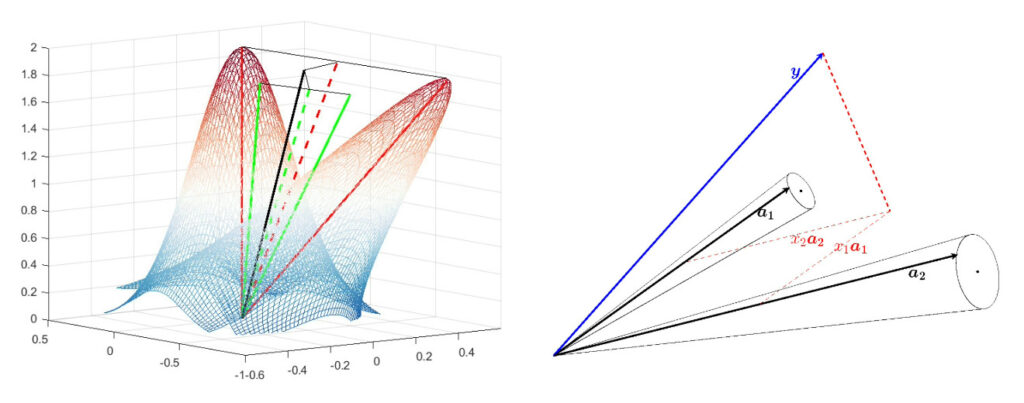
Infinite set Dictionary Learning can be used as an unsupervised anomaly detection method by learning the dictionary on an unlabeled training set and using the representation error to distinguish between normal signals and anomalies in the test set.

Experimental validation of the methods was performed on more than 30 real datasets, which cover a wide range of signal types (images, time-series and tabular), varying anomaly ratios and dataset dimensions. Results show that infinite set Dictionary Learning not only outperforms classical Dictionary Learning, but also most state of the art anomaly detection methods.

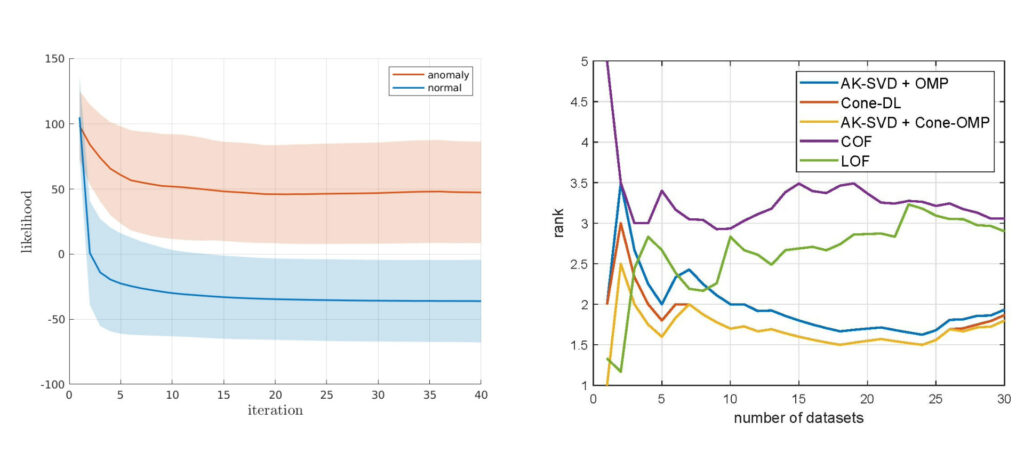
The left side of the figure below shows that indeed the learning procedure with Gaussian atoms is capable of differentiating between normal signals and anomalies. 

The right side of the figure shows the ranking of the cone atom method among classical Dictionary Learning and the two best performing state of the art anomaly detection algorithms.

The software package (see also here), written in Python, contains algorithms for computing both the dictionary update and sparse representation computation steps for both infinite set atoms methods.